Protecting Legacy Encryption from Quantum Computing: A Possible Solution.
The advent of quantum computing (QC), if it happens, will break nearly every practical application of cryptography in use today, making e-commerce and many other digital applications insecure.
Symmetric algorithms used for encryption, like AES, are still thought to be safe (with sufficient key length – e.g. AES-256 or larger); however, current asymmetric algorithms like RSA and ECDSA (Elliptic Curve Digital Signature Algorithm) will be rendered essentially useless once quantum computers reach a certain scale.
Therefore, much encrypted information that is around today, or over the coming years, will probably be susceptible to decryption one day in the future once quantum computers are generally available (if they will be available at all). The challenge is particularly severe for governments, who have large amounts of secret data with a long "intelligence life" – i.e. it needs to be kept secret for 25 years or more for national security reasons. Protection of this legacy data is not a simple problem, because of both the complexity (this data has been encrypted over the years with a menagerie of cryptographic tools) and the sheer volume of data to be protected.
Mathematicians within academia and government are working on a number of candidate "quantum-resistant" algorithms that cannot be broken using quantum computers; these algorithms comprise what is known as post-quantum cryptography.
However, it is not a good idea to rush to re-encrypt this legacy data with these new algorithms because:
- We need time to improve the efficiency of post-quantum cryptography: current algorithm implementations are prototypes and not ready for a large-scale production deployment.
- We need time to build confidence in post-quantum cryptography: like any cryptographic algorithm, it may take years to find and sort out all possible vulnerabilities. And some of these vulnerabilities may not be discovered unless a large-scale quantum computer is at hand.
- We need time to improve the usability of post-quantum cryptography: current algorithms require domain-specific expertise to be implemented.
In short, we are not yet prepared for the world to switch to post-quantum cryptography.
What is to be done?
I believe that the following solution is feasible to tackle the legacy-encryption problem, and it can be readily implemented. It relies on a class of cryptographic algorithms known as secret sharing.
Secret sharing (also called secret splitting) refers to methods for distributing a secret amongst a group of participants, each of whom is allocated a share of the secret. The secret can be reconstructed only when a sufficient number, of possibly different types, of shares are combined together; individual shares are of no use on their own.
To be specific, the secret is split into N shares in such a way that one needs at least M shares, with M ≤ N, to reconstruct the secret; an adversary that has less than M shares has the same information as somebody with no shares whatsoever. An everyday example is a bank safety deposit box: two keys are needed to open the box (M=N). Secret sharing schemes can be thought of safety deposit boxes with N locks wherein at least M ≤ N keys are needed to open the box.
Secret sharing was invented independently by Adi Shamir and George Blakley in 1979.
A key characteristic of several secret-sharing schemes is that they can be proven to be information-theoretically secure: they cannot be broken even if the adversary has unlimited computing power. One such scheme is Shamir's Secret Sharing (which is proven to provide also perfect security in that having less than the requisite number of shares of the secret provides no information whatsoever about the secret). Another such scheme is Rabin's Information Dispersal Algorithm (IDA).
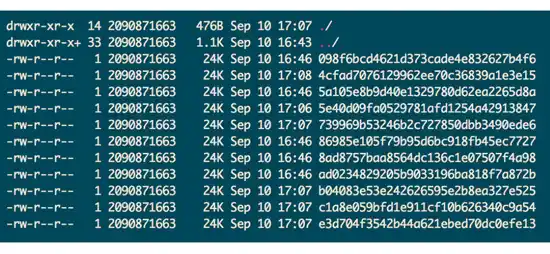
The solution to the legacy-encryption problem that I propose would work as follows: take a legacy encrypted file, split it (without decryption) using an (N,M) secret sharing scheme, and scatter the shares among different N computer hosts that form part of a network of with K hosts, with K ≫ N; the scheme will necessitate of a key that will keep track of which hosts have been used. In addition, the filename of the different shares should reveal nothing about their content; for example, the filename could be the MD5 hash of the file contents. Thus, an adversary that gains access to a host will only see files as shown in Figure 1
and the contents of the key will look something like Figure 2,

Where the first column lists the host name and the second column lists the name of the share residing in that host.
Thus, an adversary that breaks into a host used to store file shares will have not knowledge whatsoever of which shares correspond to which files, unless he has access to the key (like in any other cryptographic algorithm the safeguarding of the key is critical).
Moreover, one could reshuffle the location of the shares at fixed time intervals to add entropy to the scheme (while regenerating the key). This key itself could be split using a Secret Sharing scheme for added security. If an information-theoretically secure Secret Sharing scheme is used, and adversary will need to break into at least M hosts to be able to recover the encrypted secret (in addition to getting hold of the key file).
This solution has advantages and drawbacks.
One advantage is that it is readily implemented with today's technology once a Secret Sharing scheme is chosen; another is that upon detection that P hosts, P < M, have been compromised, the compromised shares could be replaced with others without having to replace all the shares and without having to reconstruct the secret. Also, by choosing a scheme with M < N redundancy is built into the scheme: up to N-M hosts can be disabled without impairing the ability to recover the secret (for example, N=10, M=5 will provide 50% redundancy). Last, but not least, decryption and re-encryption is not necessary.
One major disadvantage is that if a perfect-security scheme is used, such as Shamir's, the size of the shares is the same as the size of the secret; therefore, if a secret of size L is split into N shares, the required storage is N∙L. This can be alleviated somewhat if some security is given up using a scheme such as Rabin's IDA; the storage requirements of Rabin's scheme scales as N∙L/M.
Another limitation is that these schemes rely on the use of prime numbers, and if a secret of size L is to be split, a prime of L bits is needed. The largest known prime as of the time of this writing has 74,207,281 bits, thus limiting the size of the secret to about 9 MB. This limit can be overcome by breaking a large secret into pieces of size less than the largest prime, and then splitting these pieces with the Secret Sharing scheme chosen.
The above is a rough outline, but it captures the essence of the proposed solution. Many embellishments and tweaks are possible.
This scheme is not meant to replace post-quantum cryptography; it is a very specific solution to a very specific problem, while post-quantum cryptography has much wider goals and applications.
This being said, giving the level of technological readiness I believe that it is worth pursuing feasibility studies. Moreover, if implemented today, it can add an extra layer of protection against current adversarial capabilities.